Representación vectorial de textos (Parte 2) TF-IDF¶
NLP - Analítica Estratégica de Datos¶
Fundación Universitaria Konrad Lorenz
Docente: Viviana Márquez vivianam.penama@konradlorenz.edu.co
Clase #5: Marzo 18, 2021
Retroalimentación taller 3 \& 4¶
⌛ En la clase anterior¶
- Herramientas específicas de pre-procesamiento de texto en NLP
- Palabras vacías
- Tokenización
- Stemming
- Lematización
- Etiquetado gramatical
- Repaso de Feature Engineering en Machine Learning
- Representación de datos en forma numérica
- Espacio semántico vectorial
- Métodos de vectorización
- One-Hot Encoding
- Bag of Words
- Bag of N-Grams
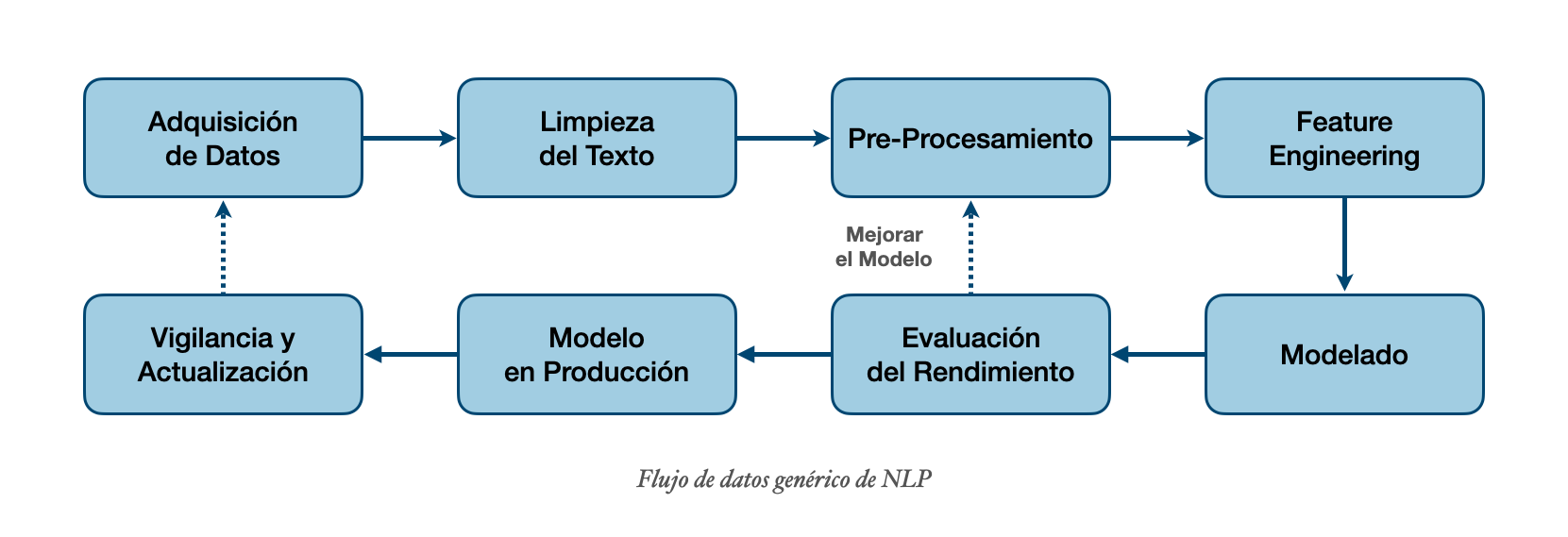
Feature Engineering para NLP¶
Representación vectorial de textos¶
- Existen varios métodos
- Lo que diferencia un método del otro es qué tan bien captura las propiedades lingüísticas del texto que representa y la cantidad de espacio que ocupa en memoria
- Métodos más populares:
- One-Hot Encoding
- Bag of Words (Bolsa de palabras)
- Bag of N-Grams (Bolsa de n-gramas)
- TF-IDF
- Word embeddings (word2vec)
- CBOW (Bolsa de palabras continua)
- SkipGram
🚀 Hoy veremos...¶
Continuación de los métodos de vectorización
- TF-IDF
Medidas de similitud
- Distancia Euclidiana
- Distancia del coseno
- Distancia de Jaccard
- Distancia de Levenshtein
🛠️ TF-IDF¶
- En los métodos que vimos en la clase pasada no hay ninguna noción de que algunas palabras del documento sean más importantes que otras
- TF-IDF (Term Frequency, Inverse Document Frequency) se ocupa de este tema
- Busca cuantificar la importancia de una palabra relativa a las otras palabras del documento y del corpus
- Se usa frecuentemente en los sistemas de recuperación de información y algoritmos de agrupación
- Entre más ayuda una palabra a distinguir un documento de los demás, más alta va a ser su puntuación TF-IDF
In [112]:
import re
import pandas as pd
import numpy as np
corpus = {'D1': 'in the new york times in',
'D2': 'the new york post',
'D3': 'the los angeles times'}
corpus = pd.DataFrame.from_dict(corpus, orient='index', columns=['texto'])
corpus
Out[112]:
TF: Term Frequency¶
- Frecuencia de términos: Contar el número de ocurrencias de una palabra en un documento, dividido por el número de palabras en ese documento
- $t$ = término
- $d$ = documento
In [113]:
corpus['d'] = corpus.texto.apply(lambda val: len(val.split()))
corpus
Out[113]:
In [114]:
from sklearn.feature_extraction.text import CountVectorizer
count_vect = CountVectorizer()
bow_rep = count_vect.fit_transform(corpus['texto'].values)
In [115]:
# Contar el número de cada una de las palabras en el documento
tf = pd.DataFrame(bow_rep.toarray())
tf.columns = count_vect.get_feature_names()
tf.index = corpus.index
tf = tf.T
In [116]:
tf = tf.div(corpus['d'], axis=1).round(3)
tf
Out[116]:
In [ ]:
In [ ]:
👮 Pop Quiz¶
- ¿Cuál es el valor máximo de $tf(t,d$)?
DF: Document Frequency¶
- La frecuencia de términos es más alta para palabras frecuentemente usadas en un documento
- Frecuencia en documentos: Es el número de documentos que tienen esa palabra sobre el número total de documentos
- $t$ = término
- $N$ = número de documentos en el corpus
In [117]:
# En cuántos documentos aparece cada una de las palabras, dividido por la cantidad de documentos
df = {}
for palabra in count_vect.get_feature_names():
suma = corpus['texto'].apply(lambda val: palabra in val).sum()
df[palabra] = suma
df = pd.DataFrame.from_dict(df, orient="index", columns=['doc_count'])
N = corpus.shape[0]
df['df'] = df['doc_count']/N
df
Out[117]:
- La frecuencia en documentos es más alta para palabras usadas en muchos documentos
- Por otro lado, una palabra específica a algún documento va a tener frecuencia de término muy baja
- Como el objetivo es distinguir un documento del otro, queremos resaltar las palabras usadas frecuentemente en un documento pero penalizarlas si están presentes en todos los documentos. A esto se le llama la puntuación TF-IDF
Inicialmente, $$tfidf(t,d,N) = \dfrac{tf(t,d)}{df(t,N)}$$
Pero esto no nos da un buen puntaje. La fórmula mejorada es:
Cuando $t$ está en todos los documentos, $idf$ es $\log(1) = 0$
Esto tiene sentido ya que una palabra que está en todos los documentos es muy mala para distinguir entre documentos
In [125]:
df['idf'] = 1/df['df']
df['log_idf'] = np.log10(df['idf'])
df
Out[125]:
In [123]:
tfidf = df.join(tf)
tfidf["tfidf_d1"] = tfidf['D1'] * tfidf['log_idf']
tfidf["tfidf_d2"] = tfidf['D2'] * tfidf['log_idf']
tfidf["tfidf_d3"] = tfidf['D3'] * tfidf['log_idf']
tfidf[['tfidf_d1', 'tfidf_d2', 'tfidf_d3']]
Out[123]:
In [132]:
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vect = TfidfVectorizer()
tfidf = tfidf_vect.fit_transform(corpus['texto'].values)
tfidf_matrix = pd.DataFrame(tfidf.toarray(), columns=tfidf_vect.get_feature_names())
tfidf_matrix.index = corpus.index
tfidf_matrix.T.round(3)
Out[132]:
- Hasta el momento, las representaciones vectoriales de texto que hemos vistos tratan las unidades lingüísticas como unidades atómicas
- Los vectores son dispersos
- Tienen problema con palabras fuera del vocabulario
-Con representaciones distribuidas, como word2vec, podemos crear representaciones densas y bajas en dimensión que capturan similitudes distributivas entre palabras
Medidas de similitud¶
¿Qué tan parecidos son los documentos?
In [135]:
n1 = "La compañía Boring de Elon Musk construirá una conexión de alta velocidad en el aeropuerto de Chicago"
n2 = "La compañía Boring de Elon Musk construirá un enlace de alta velocidad al aeropuerto de Chicago"
n3 = "La empresa Boring de Elon Musk aprobó la construcción del tránsito de alta velocidad entre el centro de Chicago y el aeropuerto O'Hare."
n4 = "Tanto la manzana como la naranja son frutas"
corpus = {'n1': n1,
'n2': n2,
'n3': n3,
'n4': n4}
corpus = pd.DataFrame.from_dict(corpus, orient='index', columns=['texto'])
corpus
Out[135]:
In [143]:
import re
from nltk.corpus import stopwords
stopwords_sp = stopwords.words('spanish')
def pre_procesado(texto):
texto = texto.lower()
texto = re.sub(r"[\W\d_]+", " ", texto)
texto = texto.split() # tokenización
texto = [palabra for palabra in texto if palabra not in stopwords_sp]
texto = " ".join(texto)
return texto
corpus['pp'] = corpus['texto'].apply(lambda val: pre_procesado(val))
corpus
Out[143]:
In [162]:
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vec = TfidfVectorizer()
tfidf = tfidf_vec.fit_transform(corpus['pp'].values)
tfidf_matrix = pd.DataFrame(tfidf.toarray())
tfidf_matrix.columns = tfidf_vec.get_feature_names()
tfidf_matrix.index = corpus.index
tfidf_matrix = tfidf_matrix.T
tfidf_matrix
Out[162]:
In [165]:
from sklearn.metrics.pairwise import euclidean_distances
dist_euc = euclidean_distances(tfidf_matrix.T.values)
dist_euc = pd.DataFrame(dist_euc, columns = tfidf_matrix.columns, index=tfidf_matrix.columns)
print(dist_euc)
corpus
Out[165]:
In [170]:
from sklearn.metrics.pairwise import cosine_distances
dist_cos = cosine_distances(tfidf_matrix.T.values)
dist_cos = pd.DataFrame(dist_cos, columns = tfidf_matrix.columns, index = tfidf_matrix.columns)
dist_cos
Out[170]:
Medidas de similitud: Distancia de Jaccard¶
- Jaccard Similarity = (Intersection of A and B) / (Union of A and B)
In [176]:
def jaccard_distance(list1, list2):
s1 = set(list1)
s2 = set(list2)
resultado = 1 - len(s1.intersection(s2)) / len(s1.union(s2))
return resultado
jaccard_distance(corpus.iloc[0]['pp'].split(), corpus.iloc[3]['pp'].split())
Out[176]:
Medidas de similitud: Distancia de Levenshtein¶
- Es el número mínimo de operaciones requeridas para transformar una cadena de caracteres en otra
- Se usa en los correctores de ortografía
Ejemplo
La distancia de Levenshtein entre "casa" y "calle" es de 3 porque se necesitan al menos tres ediciones elementales para cambiar uno en el otro.
- casa → cala (sustitución de 's' por 'l')
- cala → calla (inserción de 'l' entre 'l' y 'a')
- calla → calle (sustitución de 'a' por 'e')
In [180]:
import nltk
nltk.edit_distance(corpus.iloc[0]['pp'].split(), corpus.iloc[3]['pp'].split())
Out[180]:
🤓 Recapitulando: Hoy aprendímos...¶
- TF-IDF
Medidas de similitud
- Distancia Euclidiana
- Distancia del coseno
- Distancia de Jaccard
- Distancia de Levenshtein
🚧 ✋ Expectativas del Proyecto Final¶
Modo:
- Máximo 3 personas por grupo
- Exposición ~10 min y repositorio de GitHub
- ABRIL 15 - Plan de Proyecto (Documento con descripción del proyecto)
- JUNIO 3 - Entrega Proyecto
- JUNIO 3 y 10 - Exposiciones (La fecha puede cambiar)
Proyecto:
- Los datos pueden ser personales, del internet, o de su empresa (pedir permiso).
- Tener objetivo claro
- Pre-procesamiento
- Modelo de NLP/Machine Learning
- Visualización
Ideas para conseguir datos:
- Personales: Diario, Blog, WhatsApp, Twitter, Slack.
- Del internet:
- Scraping de Twitter, portal de noticias, página de canciones, Wikipedia, forum.
- Github: Política
- [Otro recurso] (https://lionbridge.ai/datasets/22-best-spanish-language-datasets-for-machine-learning/)
- Empresa
¡Tiempo de taller!¶
Taller # 5: Representación vectorial de textos (Parte 2)
Fecha de entrega: Marzo 25, 2021. (Antes del inicio de la próxima clase)
